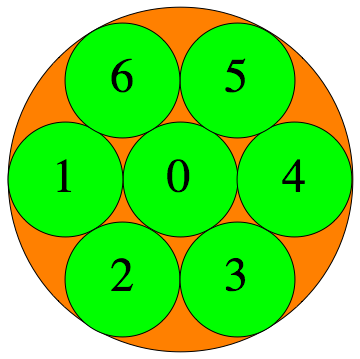
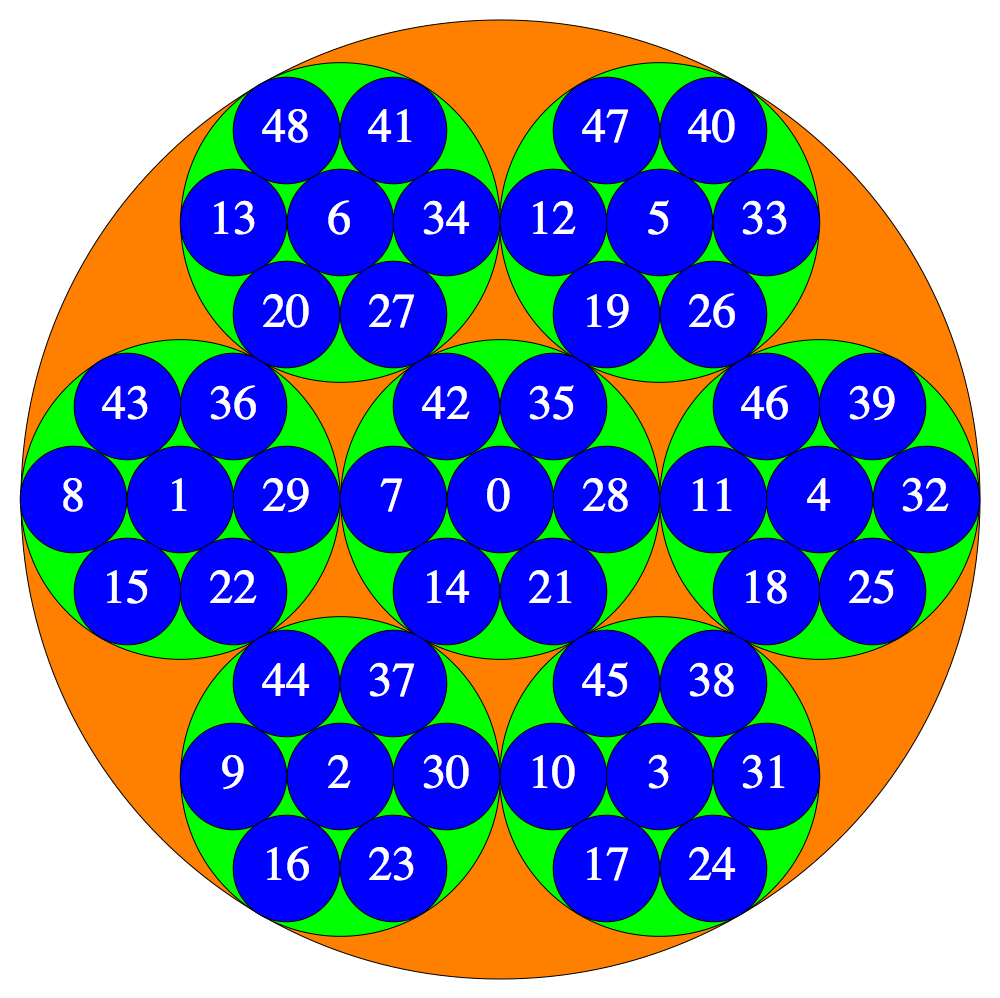
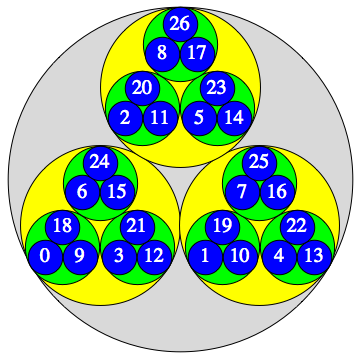
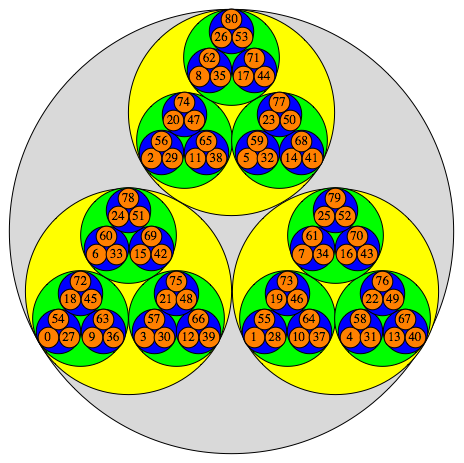
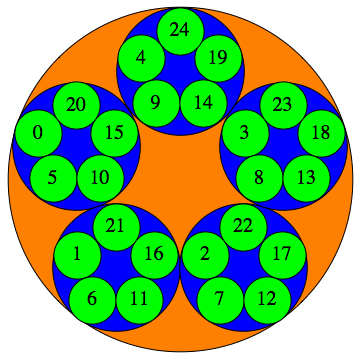
The $p$-adic integers $\mathbb{Z}_p = \varprojlim \mathbb{Z}/p^n\mathbb{Z} $ are a compact, totally disconnected Hausdorff space, i.e., a Stone space. The figures show the clopen (closed and open) subsets $a+p^n \mathbb{Z}_p$ for $p=3, 5, 7$ and $n=1,2,3,\dots$
$p=3$ :
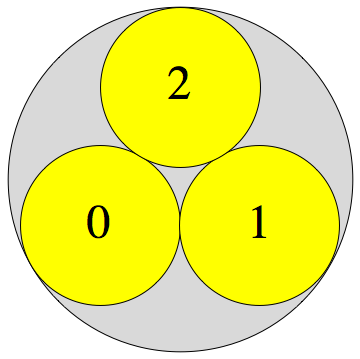
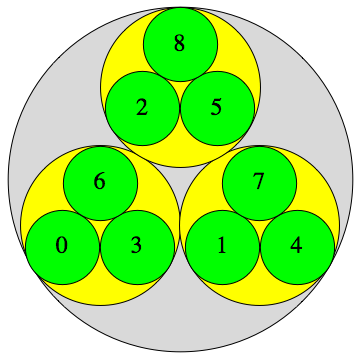
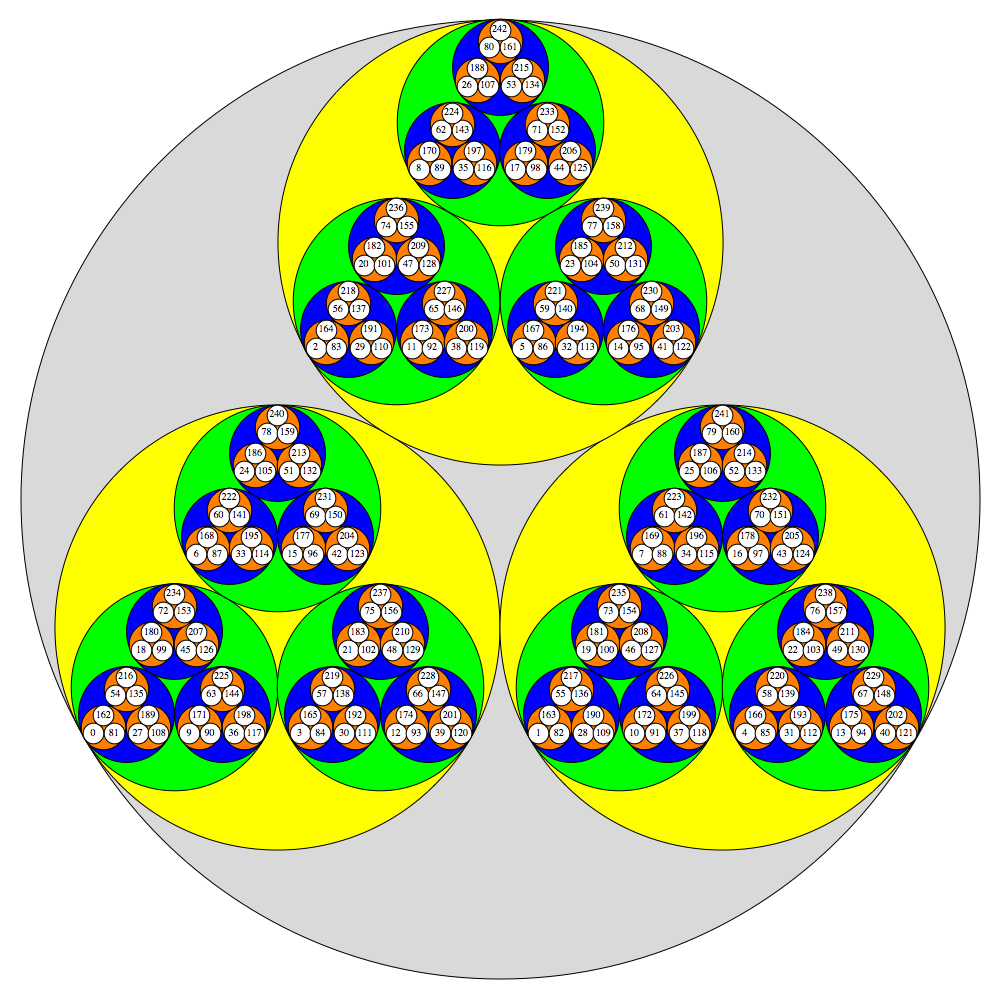
$p=5$ :
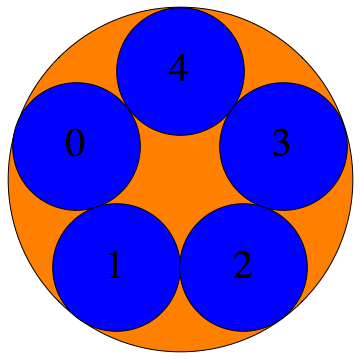
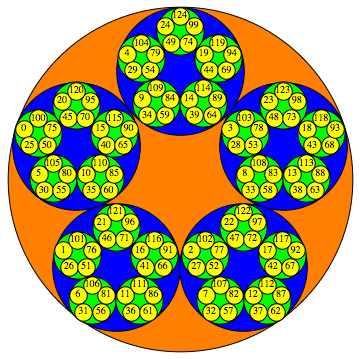
$p=7$ :